What is Poisson’s Ratio? Any prior concept! We will explain the definition, meaning along with the equation or formula and a lot of examples. In this article, we will also include the standard value of Poisson’s ratio of steel, concrete, wood, aluminium, etc. widely used materials. Let’s explore this Ratio!
What is Poisson’s Ratio? Definiton & Meaning
Let’s get into the basics of Poisson’s ratio along with definition, meaning & example.
Basics of Poisson’s Ratio
In any industry, whether it is manufacturing or automobile, or electronics, there are various kinds of materials used and all those materials need to be tested before the final application. For example, I-beams, pipes, etc.
Basically, the strength of each material needs to be tested by stretching of compressing to check its suitability as well as safe usage. Now, take a bar to get a rough idea and stretch it along the length of the bar. So, it is obvious that you have observed few key things,
- Due to the force, the bar will be extended along the length. Note that, the force is applied along the length.
- The increase in length means nothing but elongation. As it is along the longitudinal direction, the strain (change in length/original length) produced in this direction is called longitudinal strain or axial strain.
- As there is some elongation, so, definitely there will a compression perpendicular to the application of force. This compression is across the transverse direction or across the width of the bar. The strain (change in width/original width) is called lateral or transverse strain happens.
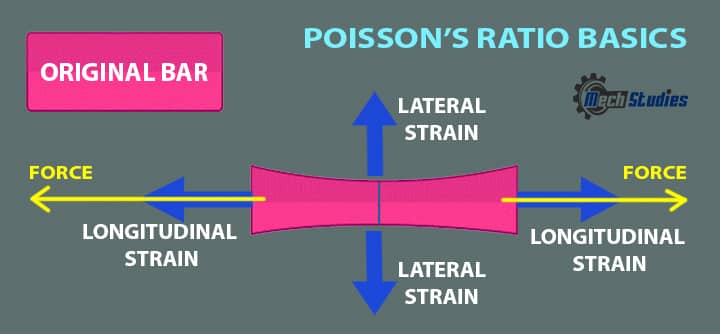
Now, this Longitudinal Strain and lateral strain are different for different kinds of materials and it is required to know so that materials can be used for the right application. Here, the function of Poisson’s ratio comes which indicates the relationship between these two strains for each material.
Poisson’s Ratio Example & Explanation
We can understand the Poisson ratio with a very simple example. We all use rubber and it is readily available in our house. Take one piece of rubber strip and stretch it. Remember, the stretching should be along the length. It is easy. Isn’t it? So, you will see an increase in the length of the rubber strip. What do you think here? Let’s get in the reason,
- Application of force on the rubber strip.
- Force is along the length.
- The length of the rubber strip is increased. So, longitudinal strain is generated.
- The rubber strip thickness is reduced i.e. lateral strain is generated.
Now, these two strains as well as their relationship reflects in Poisson’s ratio.
Poisson’s Ratio Definition & Poisson’s Effect
The Poisson’s ratio is the most important factor in the material selection which is defined as the ratio of the lateral strain to that of the longitudinal strain in the direction of the stretching force. This is known as Poisson’s effect.
- This ratio implies the basic material property of any materials.
- It is different for different materials.
- It is basically a constant value for specific materials.
- It is considered within the elastic limit.
- The value of this ratio is negative for isomers and negative for anisometric materials.
This ratio is denoted normally by the Greek letter ν (nu) .
Only isomers are discussed here. Now,
- εd = Lateral strain or Transverse Strain
- εl = Longitudinal or Axial strain
Hence, as per definition, Poisson’s Ratio, ν = (-) εd / εl
[(-) Negative sign is used to imply that there is a decrease in transverse direction during the elongation]
What does Poisson ratio of 0.5 mean?
We have seen that Poisson’s ratio is 0.3, 0.4, or 0.5, etc. Now, what does it mean? It means a factor that implies that deformation happens due to force application on the material. In this deformation, the lateral strain is 0.5 times the longitudinal strain.
History
Mr. Siméon Poisson has invented the basic concept of this ratio and it is named Poisson ratio from his name.
Poisson’s Ratio Equation & Formula
We will take a rubber stick of cylindrical shape and derive the equation or formula of the Poisson ratio.
Consideration
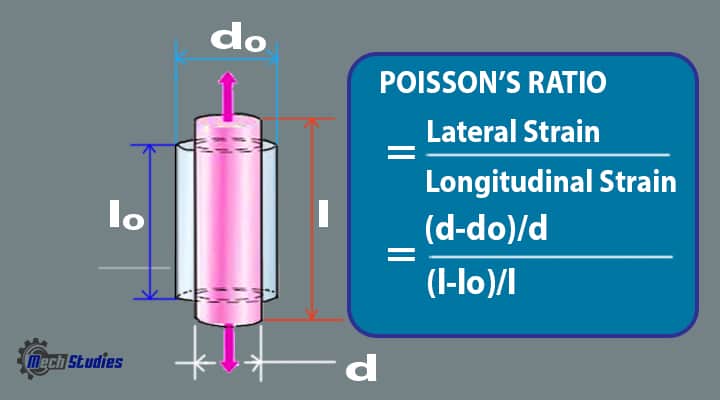
Now, apply a Force on the rubber stick along the length. Due to this application of force, the length of the rubber stick will be increased and the diameter will be decreased. Assume,
- F = The Force which is applied along the length
- lo = The length of rubber stick before force application
- do = The diameter of rubber stick before force application
- l = The increased length after force application
- d = The decreased diameter after force application
- Δl = Change (increase) in length (l-lo)
- Δd = Change (decrease) in diameter (d-do)
Diagram
We will see the below diagram to understand Poisson’s ratio formula & equation,
Poisson’s Ratio Formula or Equation Deduction
We have already learned the definition of the Poisson Ratio, We can say,
Poisson Ratio can be written as,
ν = – Lateral or Transverse Strain/Longitudinal or Axial Strain
Lateral or Transverse strain means,
= change in diameter/original diameter
= Δd/ d
= (d-do)/ d
Longitudinal or Axial Strain means
= change in length/original length
= Δl/ l
= (l-lo)/ l
Hence, we write,
Poisson’s Ratio,
ν = (-)[(d-do)/ d]/[ (l-lo)/ l]
ν = – l(d-do)/d(l-lo)
This is the basic derivation of Poisson’s Ratio Equation or Formula.
Properties of Poisson’s Ratio
Poisson’s Ratio Unit
Poisson’s Ratio (unit)
= Lateral or Transverse Strain (unit)/Longitudinal or Axial Strain (unit)
Now,
- Strain (unit) = change in dimension (unit)/original dimension (unit).
- Or, unit of strain = unit of dimension/unit of dimension
- Or, unit of strain = unitless
Transverse strain = No unit
Longitudinal strain = No unit
Hence, The unit of Poisson’s Ratio
= no unit / no unit
= no unit i.e. unitless
Is it Scalar or Vector?
It is a scalar quantity, as no direction is required to mention.
Range
Normally, Poisson’s ratio varies in the range of -1.0 to +0.5. However, for anisometric materials, the value can be more than 0.5 as well.
Poisson Ratio vs Temperature
Now, what do think about the relationship between Poisson Ratio and temperature? We know two conditions,
- Cold condition
- Hot condition
Lateral and longitudinal strain will change simultaneously in cold or hot conditions. So, it seems that Poisson’s ratio will not be changed in these conditions.
But different materials behave differently with temperature and normally it is observed that the Poisson ratio slightly decreases with temperature.
Negative or Positive
When a material undergoes a longitudinal strain under tensile stress, the length will be increased. This deformation or longitudinal strain will be (+) POSITIVE.
Compressive deformation or lateral strain means a decrease in width under stress. Here, decrease means (-) NEGATIVE.
Hence, Poisson’s Ratio represents = Negative/Positive = Negative.
[ (-) ve means here decrease in transverse direction during elongation]
This negative sign is applicable to all isotropic materials only.
But what sign will you refer to the anisotropic materials? Will it be the same? No! It will be different, the inter-atomic structure is re-arranged under tensile stress and transverse strain will be positive.
Hence, it will be (+) POSITIVE in this case!
Poisson’s ratio can be greater than 1
Normally, we got the idea that the value of Poisson’s ratio is a maximum of 0.5. So, what do you think, can it be greater than 1? Yes. it can be. This value can be more than 1 for anisotropic materials like polyurethane foam.
Maximum Poisson’s ratio
The maximum Poisson’s ratio is 0.4999. This value is for rubber (isotropic materials ).
).
Poisson’s Ratio of Steel, Aluminium, Concrete, Rubber & Others
Let’s see the Poisson’s ratio of steel, aluminium, concrete, rubber, wood along with other few materials which are widely used in various industries.
Poisson’s Ratio of Steel (0.30)
Poisson’s ratio for steel is 0.3 means a factor that implies that deformation happens due to force application on the steel. In this deformation, the lateral strain on the steel is 0.3 times the longitudinal strain on the same material.
Poisson’s Ratio Aluminium (0.32)
Poisson’s ratio for aluminium is 0.32 means a factor that implies that deformation happens due to force application on the aluminium. In this deformation, the lateral strain on the aluminium is 0.32 times the longitudinal strain on the same material.
Poisson’s Ratio for Concrete (0.1 to 0.2)
Poisson’s ratio for concrete varies from 0.1 to 0.2 means a factor that implies that deformation happens due to force application on the concrete. In this deformation, the lateral strain on the concrete varies from 0.1 to 0.2 times the longitudinal strain on the same material.
Poisson’s Ratio of Rubber (0.4999)
Poisson’s ratio for rubber is 0.4999 means a factor that implies that deformation happens due to force application on the rubber. In this deformation, the lateral strain on the rubber is 0.4999 times the longitudinal strain on the same material.
Poisson’s Ratio of Wood (0.2 to 0.4)
Poisson’s ratio for wood varies from 0.2 to 0.4 means a factor that implies that deformation happens due to force application on the wood. In this deformation, the lateral strain on the wood varies from 0.2 to 0.4 times the longitudinal strain on the same material.
Poisson’s Ratio of Cork (0.0)
The value of the Poisson ratio of cork is simply zero (0) and it means cork will not exhibit any transverse strain under tensile stress/stretching.
Other materials
Let’s see the brief table to get an idea about Poisson ratio of other materials,
| Material | Poisson Ratio |
| Bronze | 0.34 |
| Brass | 0.331 |
| Clay | 0.30–0.45 |
| Carbon Steel | 0.27–0.30 |
| Copper | 0.33 |
| Concrete | 0.1–0.2 |
| Cast iron | 0.21–0.26 |
| Cork | 0 |
| Granite | 0.2 – 0.3 |
| Foam | 0.10–0.50 |
| Inconel | 0.27-0.38 |
| Gold | 0.42–0.44 |
| Glass | 0.18–0.3 |
| Ice | 0.33 |
| Limestone | 0.2-0.3 |
| Lead | 0.431 |
| Molybdenum | 0.307 |
| Marble | 0.2 – 0.3 |
| Magnesium alloy | 0.252–0.289 |
| Monel | 0.315 |
| Nickel Steel | 0.291 |
| Nickel | 0.31 |
| Polystyrene | 0.34 |
| Platinum | 0.39 |
| Rubber | 0.48-0.4999 |
| Silver | 0.37 |
| Sand | 0.20–0.455 |
| Stainless steel | 0.30–0.31 |
| Tungsten | 0.28 |
| Titanium | 0.265–0.34 |
| Tin | 0.33 |
| Wrought iron | 0.278 |
| Zinc | 0.331 |
How to Measure Poisson’s Ratio?
After getting the values of Poisson ratio for different materials, let’s check how this value is measured.
Let’s try to understand,
- Definitely, you need equipment that helps to deform the material as well as to measure the deformation precisely. Extensometer is a machine that is widely used for this.
- Now, take a specimen or material for which the Poisson ratio to be measured.
- Measure the original length of the specimen.
- Measure the original width or diameter of the specimen.
- After basic measurement, the specimen needs to be mounted in the extensometer.
- After proper mounting, force to be applied along the length for the extension.
- Measure the length after force application. The machine will give the data.
- Measure the width after force application. The machine will give the data.
Now, in the final stage, calculate the transverse strain & longitudinal strain and divide transverse strain to longitudinal strain to get the value.
Application of Poisson’s Ratio
The Poison ratio is applied in many industries, like –
Material Strength: In all industries, various materials are used to make equipment. It is from the turbine, pump, compressor to small electronics. Hence, the strength of all those materials is understood from this ratio. This ratio helps to select a suitable material based on the applications.
Piping & Pipeline industries: Piping and pipelines are the most used systems in various many industries like thermal power plants, nuclear power plants, hydroelectric power plants, water projects, HVAC systems, oil & gas projects, etc. This ratio helps to select proper piping as well pipeline materials based on the applications.
Cork used for bottle sealing: Cork’s Poisson ratio is 0. So, based on this value is it used as perfect sealing of bottles.
Automobile Industries: There are so many materials used in the automobile industry. Hence, types of metals, as well as the strength of materials, are selected from this ratio.
Aviation Industries: In the aviation industry, lightweight with high-strength materials are used, hence, the Poisson ratio plays an important factor to select the materials.
Calculation on Poisson’s Ratio
Question
A metallic rod is subjected to a tensile force. The diameter of the rod is 6mm. The applied force is 6 x 103 N. Decrease in diameter by 3.6 x 10-4 cm. Calculate the Poisson ratio. If the Young modulus of the metallic rod is 7 x 1010 N/m2.
Given Data: Diameter of metallic rod = d = 6 mm = 6 x 10-3 m
Area of metallic rod, A = πd2 = 3.14 x (6 x 10-3)2
Applied force value, F = 6 x 103 N
Change in diameter due to force = Δd = 3.6 x 10-4 cm = 3.6 x 10-6 m
Young modulus of the metal, Y = 7 x 1010 N/m2
Calculate: Find out the value of Poisson Ratio.
Solution
Poisson ratio (ν) = (-)Lateral strain / Longitudinal strain
Lateral strain
= Δd /d
= 3.6 x 10-6 / 6 x 10-3
= 3.6 x 10-3/6
= 6 x 10-4
Now, we have to find out the longitudinal strain, to calculate the Poisson ratio.
So, what is the method to find out this?
Here, we can get this value from the young modulus!
We all know that,
Young modulus, Y = Longitudinal stress / Longitudinal strain
Longitudinal stress
= Force/area
= F / A
= 6 x 103 / 3.14 x (6 x 10-3)2
So,
Y = Longitudinal stress / Longitudinal strain
7 x 1010 = [6 x 103 / 3.14 x (6 x 10-3)2] / Longitudinal strain
Longitudinal strain = 6 x 103 / 3.14 x (6 x 10-3)2/7 x 1010
Longitudinal strain
= 6 x 103 / 3.14 x (6 x 10-3)2 x 8 x 1010
= 6 x 103 / 3.14 x 6 x 7 x 104
= 1 / 3.14 x 7 x 10
= 0.00455
= 4.55 x 10-3 m
So, Poisson Ratio, ν
=7 x 10-4 / 4.55 x 10-3
= 1.5384 x 10-1
= 0.154 (result)
So, the value of the ratio is 0.154
Code & Standards for Poisson Ratio
To measure or calculate this ratio, there is one standard
ASTM E132 Standards for Poisson ratio measurements
Conclusion
Hence, I hope you enjoyed this article as well as the basic concept of Poisson Ratio, its definition, meaning, formula, equation, examples, a small exercise, etc. Any doubt, please let us know. Happy reading!
